DeepSeek AI发布DeepSeekMath-V2：在Putnam 2024竞赛中获得118/120分的开放权重数学模型。

DeepSeek AI 推出了 DeepSeekMath-V2，这是一个针对自然语言定理证明和自我验证进行优化的开放weights大型语言模型。该模型基于 DeepSeek-V3.2-Exp-Base 构建而成，作为一个 685B参数 的专家混合系统运行，并以Apache 2.0许可协议在Hugging Face上提供。

在评估中，DeepSeekMath-V2 在IMO 2025和CMO 2024上达到了 金牌水平分数，当与扩展的测试时间计算相结合使用时，在Putnam 2024上实现了 120分中的118分。

为什么最终答案奖励还不够？

大多数最近的神学推理模型使用强化学习，只在基准测试（如AIME和HMMT）上的最终答案上进行奖励。这种方法在一年的时间里将模型从弱基线推进到短回答竞赛中的饱和水平。

然而，DeepSeek研究团队指出了两个结构性问题：

正确的数字答案并不能保证正确的推理。模型可能通过代数错误得到正确的数字，但这些错误可能会抵消。
许多任务，如奥林匹克证明和定理证明，需要完整的自然语言论证。这些任务没有单一的最终数字答案，因此基于答案的奖励不适用。

因此，DeepSeekMath-V2优化了证明质量而不是纯粹的答案准确性。系统会评估证明是否完整并且逻辑清晰，并使用这种评估作为主要的学习信号。

在生成器之前训练验证器

其核心设计是验证器优先。DeepSeek研究团队训练了一个基于LLM的验证器，可以阅读问题和候选证明，然后输出自然语言分析和离散质量分数（集合{0，0.5，1}）。

初始的强化学习数据来自解决问题艺术比赛。研究团队从奥林匹克、团队选拔测试和2010年后的明确要求证明的问题中爬取了17,503个证明风格的题目。这些题目构成了冷启动RL的基础集合。候选证明来自一个被提示迭代改进其自身解决方案的DeepSeek-V3.2推理模型，这增加了细节但也产生了许多不完美的证明。人类专家使用0，0.5，1刻度根据严谨性和完整性将这些证明进行标注。

验证器是用群相对策略优化(GRPO)进行训练的。奖励有两个组成部分：

格式奖励，检查验证器输出的格式遵循固定的模板，包括分析部分和一个框中的最终分数。
分数奖励，惩罚预测分数与专家分数之间的绝对差异。

这一阶段产生了一个可以以一致方式评估奥林匹克风格证明的验证器。

https://github.com/deepseek-ai/DeepSeek-Math-V2/blob/main/DeepSeekMath_V2.pdf

元验证以控制幻觉的批评

验证器仍然可以作弊奖励。它可以输出正确的最终分数，同时在分析中发明伪问题。这会满足数字目标，但会使解释不可靠。

为了解决这个问题，研究团队引入了一个元验证器。元验证器阅读原始问题、证明和验证器分析，然后评估分析是否忠实。它评分方面，如各步骤的重新陈述、识别真实缺陷和叙述与最终分数之间的一致性。

元验证器也是用GRPO进行训练的，有自己的格式和分数奖励。它的输出，一个元质量分数，然后用作基础验证器的额外奖励项。分析中的虚构问题得到低元分数，即使最终证明分数是正确的。在实验中，这将验证在数据集上的平均元评价质量从大约0.85提高到0.96，同时保持证明分数的准确性。

自我验证的证明生成器和顺序微调

一旦验证器强大，DeepSeek研究团队就训练验证器生成器。生成器接受一个问题，并输出一个解决方案和自我分析，该分析遵循与验证器相同的标准。

生成器的奖励结合了三个信号：

验证器对生成的证明的评分。
自我报告的评分与验证器评分之间的协议。
自我分析的元验证评分。

从形式上来说，主要奖励使用weight(α = 0.76)和终端评分的权重(_β = 0.24)，乘以一个强制输出结构的格式项。这推动生成器编写验证器接受的证明，并且对存在的问题诚实。如果它声称有缺陷的证明是完美的，它将通过不和谐和低元分数丢失奖励。

DeepSeek还使用了基模型的128K令牌上下文限制。对于困难的问题，生成器通常无法在单一通过中修复所有问题，因为经过细化的证明加上分析将超出上下文。在这种情况下，系统运行顺序微调。它生成一个证明和自我分析，将它们作为上下文反馈，然后要求模型生成新的证明来修复先前检测到的问题。此循环可以重复多次，但在上下文预算下。

https://github.com/deepseek-ai/DeepSeek-Math-V2/tree/main

验证和自动标注的扩展

随着生成器的改进，它产生了更难的证明，手动标注代价高昂。为了保持训练数据的新鲜，研究团队引入了一套基于扩展验证的自动标注管道。

对于每个候选证明，系统从多个独立的验证器分析中采样，然后使用元验证器评估每个分析。如果多个高质量分析在对严重问题达成一致，则证明被标记为错误。如果没有有效的问题在元检查中存活，则证明被标记为正确。在最终的训练迭代中，此管道取代了人工标签，抽查确保与专家的一致性。

竞争和基准结果

研究团队在多个方面评估了DeepSeekMath-V2：

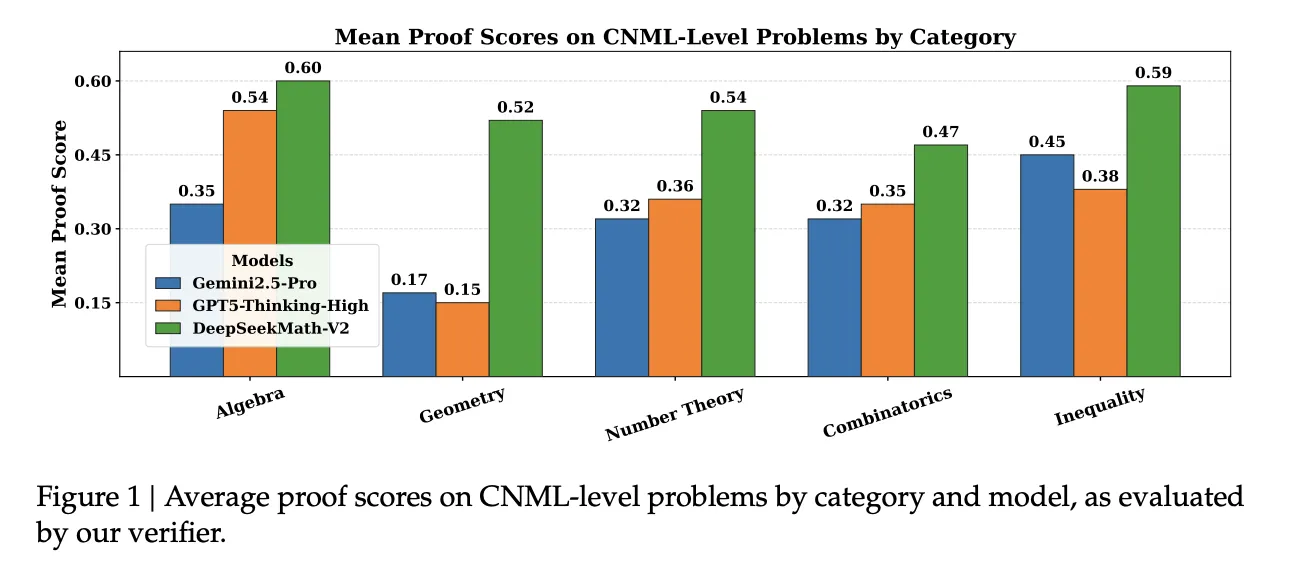
在涵盖代数、几何、数论、组合数学和不等式的91个CNML级别问题集合方面，它显示出DeepSeekMath-V2在其所测量的验证器中在每个类别上都有最高的平均证明分数，超过Gemini 2.5 Pro，GPT 5 Thinking High和DeepSeekMath-V2。

https://github.com/deepseek-ai/DeepSeek-Math-V2/blob/main/DeepSeekMath_V2.pdf

在IMO Shortlist 2024上，随着最大细化迭代次数的增加，顺序微调和自我验证提高了通过1和32个最佳质量标准。

https://github.com/deepseek-ai/DeepSeek-Math-V2/blob/main/DeepSeekMath_V2.pdf

在IMO ProofBench上，专家评估显示，DeepSeekMath-V2在基础子集上优于DeepMind DeepThink IMO Gold，在高级子集上与国际大模型竞争，明显优于其他大模型。

https://github.com/deepseek-ai/DeepSeek-Math-V2/blob/main/DeepSeekMath_V2.pdf

对于完整的比赛，它报告了以下结果：

IMO 2025：6个问题中的5个被解决，获得金牌水平。
CMO 2024：4个问题完全解决，另1个问题得到部分成绩，获得金牌水平。
Putnam 2024：12个问题完全解决，剩余问题有小的错误，获得120分中的118分，高于当年人类最佳成绩90分。

主要收获

DeepSeekMath V2是一个建立在DeepSeek V3.2 Exp Base之上的685B参数模型，旨在实现自然语言的定理证明和自我验证，并以Apache 2.0许可证作为开放weights发布。
主要创新是验证器优先的训练管道，该管道用GRPO训练的验证器和元验证器进行评分，这直接解决了正确答案和正确推理之间的差距。
接着对该验证器和元验证器进行训练的证明生成器，使用结合证明质量、与自我评估的一致性、分析忠实度以及顺序微调（在128K上下文范围内）的奖励相结合的回报，迭代地纠正证明。
通过缩放测试时间计算和大验证器预算，DeepSeekMath V2在IMO 2025和CMO 2024上达到了金牌水平性能，在Putnam 2024上得到了118分（120分中的118分），超过了那一年最佳人类得分。

编辑笔记

DeepSeekMath-V2是迈向自我验证数学推理的重要一步，因为它直接解决了正确最终答案和正确推理之间的差距，使用一个验证器、元验证器和用GRPO在奥林匹克风格证明上训练证明生成器，并在685B规模上部署以在IMO 2025、CMO 2024上达到金牌水平性能，并在Putnam 2024上得到几乎是完美的118/120分。总的来说，这次发布表明，具有开放weights的自我验证数学推理现在在竞争级问题上是实际可行的。

可以查看完整论文，HF上的模型权重和存放仓库。您可以随时查看我们的GitHub页面上的教程、代码和笔记本。还可以follow我们的Twitter并别忘了加入我们的10k+ ML SubReddit和订阅我们的时事通讯。等等！你用Telegram吗？现在你可以加入我们的Telegram群组。

文章DeepSeek AI 发布 DeepSeekMath-V2：在 Putnam 2024 上得 118/120 分的开放weights 数学模型首先出现在MarkTechPost。